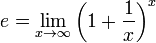Imagineu que li posem a la terra un
cinturó a l'equador ( per simplificar , suposarem que la terra és
totalment esfèrica ) . Doncs bé , la longitud d' aquest cinturó
deuria tenir una longitud de més de 40 milions de metres , anem ,
que ens sortiria una mica car . Tallem el cinturó per un punt
qualsevol ii afegim per allà un metre de cinturó més . Un cop fet
això , amb aquesta amplada extra , separem el cinturó de la terra
la mateixa distància per tots els punts . Sense fer cap càlcul i
responent intuïtivament , quanta serà l'altura que s'elevarà el
cinturó ? Podrem ficar un foli per sota ? Uhm , no sé ... ¿ I la
mà ? Si no estiguéssiu sospitant que hi ha un parany , segur que
hauríeu dit que no ...
Doncs la resposta és que es podrà
aixecar gairebé ¡ 16 centímetres ! Com és això ? Bé , si L és
la longitud inicial del cinturó en metres i R és el radi de la
terra en metres , i per tant de la circumferència que forma el
cinturó , tindrem la següent relació :
L = 2·π
(pi)·R
Ara bé , si afegim un metre al
cinturó, el nou ràdio del cinturó serà R + h, on h és
l'altura a la qual s'elevarà el cinturó uniformement del sòl ,
tenint la següent relació :
L +1 = 2·π
(pi)·(
R + h ) .
Restant ara les dues expressions
anteriors haurem de
1 = 2 · π
(pi)·h
Aclarint ara h ,
h = 1/2·π
(pi)
que aproximadament són 16 centímetres
. ¿ Sorprenent ? El problema és que un pensa que deu ser molt menys
perquè 1 metre és menyspreable al costat de més de 40 milions de
metro de cinturó . Però clar, el mateix passa amb 16 centímetres
al comparar-los amb el radi de la Terra , de fet ambdues quantitats
seran menyspreables en la mateixa proporció .