La constant matemàtica e, és un dels
més importants nombres reals. Aquest
nombre és conegut, de vegades com nombre
d'Euler o constant de Napier, utilitzat per primera vegada pel matemàtic escocès John Napier, qui va introduir el
concepte de logaritme en el càlcul matemàtic.
És
considerat el nombre per excel·lència del càlcul. El nombre e, igual que el
nombre π, i el nombre auri φ, és un irracional, no expressable per la raó de
dos enters, o bé, no pot ser expressat amb un nombre finit de xifres decimals o
amb decimals periòdics. A més, és un nombre transcendent, és a dir, que no pot
ser obtingut mitjançant la resolució d'una equació algebraica amb coeficients
racionals.
El seu valor aproximat és: e ≈ 2,71828 18284 59045 23536 02874 71352 66249
77572 47093 69995...
Origen:
El "descobriment" de la constant està acreditat a Jacob Bernoulli, qui va estudiar un problema particular de l'anomenat interès compost. Per tant, va observar que cada vegada que s'augmenta la quantitat de períodes de pagament en un factor de n (que tendeix a créixer sense límit) i es redueix la taxa d'interès en el període, en un factor de 1/n, el total d'unitats monetàries obtingudes està expressat per la següent equació:
Bernoulli va comprovar que aquesta expressió s'aproxima al valor 2,7182818 ...UM .
La definició més comuna de e és com el valor límit de la sèrie
que s'expandeix com:
Una altra definició habitual donada a través del càlcul integral és com a solució de l'equació:
Propietats:
-Càlcul
La funció exponencial f(x) = e^x és la seva pròpia derivada.
A més e és el límit d'una successió.
-Desenvolupament decimal no mostra regularitat alguna.
-Nombres complexos:
El nombre e presenta a la fórmula d'Euler un paper important relacionat amb els nombres complexos:
El cas especial amb x = π és conegut com a identitat d'Euler:
del que es dedueix que:
A més, utilitzant les lleis de la exponenciació, s'obté la formula de De Moivre.
Teresa Pons Bosch






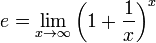



Cap comentari:
Publica un comentari a l'entrada